|
|
|
|
|
|
|
- 三角関数を理解するためには先ず「平方根」を理解して下さい。
- 関数「平方根」は正の平方根(へいほうこん)を返します。
- 別名では二乗根(にじょうこん)、自乗根(じじょうこん)。
- 英名では「Square Root」(スクエア)
- VBでは[sqr()]、エクセルで求めるならSQRT。
- 記号は√で表します。
-
| 平方根の記号 |
√a |
読みはルートエー(a)、√は根号 |
|
どのご家庭にも必ずある官製はがき、これを例にして平方根を説明します。 |
 ハガキは横幅が約10cm、高さが15cmあります。 ハガキは横幅が約10cm、高さが15cmあります。
ハガキの赤線の長さを求めるにはどうすればよいでしょう?
答えは「18.02775638」cmになります。 |
|
|
 |
- 横幅をX座標、高さをY座標をします。
- X^2剰 (10cm×10cm) = 100
- Y^2剰 (15cm×15cm) = 225
- これを足し算します。100 + 225 = 325
- エクセルならシート関数[=SQRT(325)]で答えがでます。
- この関数「SQRT」が平方根です。
- 平方根はある数字が2剰と一致する数値です。
- 例えばある数字が「4」であれば「4 = 2 × 2」つまり、2^2剰です。
- 「9」であれば3、「16」であれば4です。この「2」「3」「4」の数値が平方根です。
|
|
|
| 回数 |
個々の数値 |
式 |
| 1 |
9 |
- |
1 |
= |
8 |
9 - 1 = 8 |
| 2 |
8 |
- |
3 |
= |
5 |
8 - 3 = 5 |
| 3 |
5 |
- |
5 |
= |
0 |
5 - 5 = 0 |
- 黄色の部分は1から始まる増加していく奇数です。
- 基になる「9」から最初の奇数「1」を引きます。
- すると答えは「8」になります。
- この「8」が次の基になる数値です。
- 今度は「8」から次の奇数「3」を引きます。
- これを答えが「0」になるまで続けます。
- 回数は「3」回になります。これが平方根です。
- √9と表します。
|
|
|
| 回数 |
個々の数値 |
式 |
| 1 |
7 |
- |
1 |
= |
6 |
7-1=6 |
| 2 |
6 |
- |
3 |
= |
3 |
6-3=3 |
| 1 |
384 |
- |
41 |
= |
343 |
384-41=343 |
| 2 |
343 |
- |
43 |
= |
300 |
343-43=300 |
| 3 |
300 |
- |
45 |
= |
255 |
300-45=255 |
| 4 |
255 |
- |
47 |
= |
208 |
255-47=208 |
| 5 |
208 |
- |
49 |
= |
159 |
208-49=159 |
| 6 |
159 |
- |
51 |
= |
108 |
159-51=108 |
| 7 |
108 |
- |
53 |
= |
55 |
108-53=55 |
| 8 |
55 |
- |
55 |
= |
0 |
55-55=0 |
- 例えば「784」なような場合には、
- 数値を分けて考えます。
- 「784」の場合だと「7」と「84」に分けます。
- 「7」から始めます。
- 2回で引けなくなりました。
- 余りは「3」、それと「84」を結合した数値にします。
- 「384」を基点として回数は新たに数えます。
- 次に黄色の引く数値が変わります。
- 最後の黄色の数値は「3」でしたから今度はその数値に3の次の数値の4(3+1=4)と1から始まる奇数を結合した数値「43」から始めます。
- 「8」回で終わりました。
- 最初の「7」の方は「2」回でしたから「28」になります。
- この様に筆算で求める方法を開平法と言います。
|
|
- ハガキの
- X~2剰 (10cm×10cm) = 100
- Y~2剰 (15cm×15cm) = 225
- 二つを足すと100 + 225 = 325になります。
- 関数を使う場合は式を入れます。
- =SQRT( X^2 + Y^2 )
- スクエアと読みます。
- 答えは「18.02775638」cmになります。
|
|
|
- 「いい国つくろう鎌倉幕府(現在は1185年説もあり)」は歴史年号ですが語呂合わせ数学バージョンにもあります。
- 1~10の整数に限って言えば平方数の1と4と9以外の数値の平方根は整数にはなりません。
- 1と4と9を除く数値の平方根は円周率の「3.14・・・・」のような終わりのない数値になります(無理数という)。
|
| √1 |
1 |
整数 |
| √2 |
1.414213562 |
一夜一夜に人見頃(ひとよひとよにひとみごろ) |
| √3 |
1.732050808 |
人並みに奢れや女子(ひとなみにおごれやおなご) |
| √4 |
2 |
整数 |
| √5 |
2.236067977 |
富士山麓鸚鵡鳴く(ふじさんろくおーむなく) |
| √6 |
2.449489743 |
ツヨシ串焼くな(つよしくしやくな) |
| √7 |
2.645751311 |
菜に虫いない(なにむしいない) |
| √8 |
2.828427125 |
ニヤニヤ呼ぶな(にやにやよぶな) |
| √9 |
3 |
整数 |
| √10 |
3.16227766 |
父さん一郎兄さん(とうさんいちろーにーさん) |
|
|
<
|
|
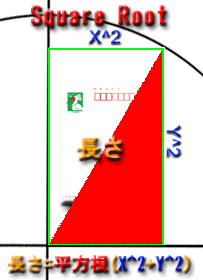 |
長さ=斜辺 |
|
|
|
|
|
ラジアンとディグリー(角度)を覚えないと三角関数は判りません。 |
- ラジアンの値は近似値。
- 角度を数値にしたものです。
- PI()=3.14159265358979 つまり円周率です。
- エクセルでは「=PI()」で求められます。
|
円周率は英語でPi
| PI()=3.14159265358979 |
| PI()*2= |
6.283185307 |
| PI()= |
3.141592654 |
| PI()/2= |
1.570796327 |
| PI()/4= |
0.785398163 |
| PI()/8= |
0.392699082 |
|
| PI()=3.14159265358979(ラジアン) |
| 数式(参照元[ラジアン]) |
答え(ディグリー) |
(ラジアン)答え |
数式(参照元[ディグリー]) |
| =DEGREES(PI()*2) |
360 |
6.283185307 |
=RADIANS(360) |
| =DEGREES(PI()) |
180 |
3.141592654 |
=RADIANS(180) |
| =DEGREES(PI()/2) |
* 90 |
1.570796327 * |
=RADIANS(90) |
| =DEGREES(PI()/4) |
45 |
0.785398163 |
=RADIANS(45) |
| =DEGREES(PI()/8) |
22.5 |
0.392699082 |
=RADIANS(22.5) |
- ラジアンで表された角度を度に変更します。
- DEGREES(角度) / ディグリー
- 使用例 DEGREES(PI()) = 180
- 上の表* 「1.570796327」ディグリー = 90度になります。
- 関数使用ではDEGREES(1.570796327) = 90
- 度単位で表された角度をラジアンに変換した結果を返します。
- RADIANS(角度) / ラジアン
- 使用例 RADIANS(270) = 4.712389 (3π/2 ラジアン)
- 上の表* 「90」ラジアン = 1.570796327 になります。
- 関数使用ではRADIANS(90) = 1.570796327
|
|









