|
|
|
|
|
|
|
- サイン・コサイン・タンジェントの他にそれらの文字の頭に「アーク」が付加する、
- アークサイン・アークコサイン・アークタンジェントがあります。
- サイン・コサイン・タンジェントはシータθ(角度)からX辺(コサイン)の長さやY辺(サイン)の長さを算出しましたが、
- アークサイン・アークコサイン・アークタンジェントはサイン・コサイン・タンジェントからシータθ(角度)を算出します。
- これらを逆三角関数と呼びます。
- 英名では Inverse Trigonometric Function
- サイン・コサイン・タンジェントの「逆数」コセカント・セカント・コタンジェントとは全く違います。混同しないように!
- 逆数とは
- "x / y" → "y / x" , "z / y" → "y / z" のように式が逆になることです。
|
- ACOS
- ARCCOS
- 数値のアークコサインを返します。
- アークコサインとは、そのコサインが 数値 であるような角度のことです。
- 戻り値の角度は、0(ゼロ) ~ PI の範囲のラジアンとなります。
- 書式
- ACOS(数値)
- 数値 求める角度のコサインの値を、-1 ~ 1 の範囲で指定します。
- アークコサインの値を度で表すには、計算結果に 180/PI() を掛けます。
- 使用例
- ACOS(-0.5) = 2.094395 (2PI/3 ラジアン)
- ACOS(-0.5) = 120 (度)
- ASIN
- ARCSIN
- 数値のアークサインを返します。
- アークサインとは、そのサインが 数値 であるような角度のことです。
- 戻り値の角度は、-PI/2 ~ PI/2 の範囲のラジアンとなります。
- 書式
- ASIN(数値)
- 数値 求める角度のサインの値を、-1 ~ 1 の範囲で指定します。
- アークサインの値を度で表すには、計算結果に 180/PI() を掛けます。
- 使用例
- ASIN(-0.5) = -0.5236 (-PI/6 ラジアン)
- ASIN(-0.5)*180/PI() = -30 (度)
- ATAN
- ARCTAN
- 数値のアークタンジェントを返します。
- アークタンジェントとは、そのタンジェントが 数値 であるような角度のことです。
- 戻り値の角度は、-PI/2 ~ PI/2 の範囲のラジアンとなります。
- 書式
- ATAN(数値)
- 数値 求める角度のタンジェントの値を指定します。
- アークタンジェントの値を度で表すには、計算結果に 180/PI() を掛けます。
- 使用例
- ATAN(1) = 0.785398 (PI/4 ラジアン)
- ATAN(1)*180/PI() = 45 (度)
- ATAN2
- 指定された x-y 座標のアークタンジェントを返します。
- アークタンジェントとは、x 軸から、原点 0 と x座標、y座標 で表される点を結んだ直線までの角度のことです。
- 戻り値の角度は、-PI ~ PI (ただし -PI を除く) の範囲のラジアンとなります。
- 書式
- ATAN2(x座標, y座標)
- x座標, 点の x 座標を指定します。
- y座標, 点の y 座標を指定します。
- 戻り値が正の数なら x 軸から反時計回りの角度を表し、負の数なら x 軸から時計回りの角度を表します。
- ATAN2(a,b) = ATAN(b/a) という関係になりますが、ATAN2 関数では、a に 0 を指定することができます。
- x座標 と y座標 が両方とも 0 である場合、エラー値 #DIV/0 が返されます。
- アークタンジェントの値を度で表すには、計算結果に 180/PI() を掛けます。
- 使用例
- ATAN2(1, 1) = 0.785398 (PI/4 ラジアン)
- ATAN2(-1, -1) = -2.35619 (-3*PI/4 ラジアン)
- ATAN2(-1, -1)*180/PI() = -135 (度)
|
関数の記号の右上に「−1」を付ける
| アークコサイン |
cos |
-1 |
| |
| アークサイン |
sin |
-1 |
| |
| アークタンジェント |
tan |
-1 |
| |
|
|
-
 |
| |
A |
B |
C |
| 1 |
角度 |
90 |
説明 |
| 2 |
RADIANS |
1.570796327 |
ラジアンを求める |
| 3 |
Cosine(x座標) |
6.12574E-17 |
|
| 4 |
Sine(y座標) |
1 |
|
| 5 |
Tangent(z座標) |
1.63246E+16 |
( = y / x ) |
| 6 |
ARCCosine(角度) |
90 |
|
| 7 |
ARCSine(角度) |
90 |
|
| 8 |
ARCTangent(角度) |
90 |
( = y / x ) |
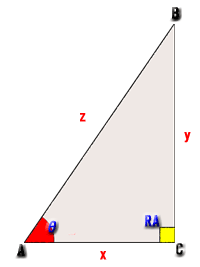
- 上記はピタゴラスの定理:1章-2D編-図解で使ったものに数式を追加したものです。
- 又上記はエクセルのに数式を入れ表示された値をそのまま写したものです。
- 下記はその数式を写しました。
- 黄色の部分を選択するか
ボタンを押してエクセルのセル「A1」に「貼り付け」てみてください
-
| |
A |
B |
C |
| 1 |
| 角度 |
90 |
説明 |
| RADIANS |
=RADIANS(B1) |
ラジアンを求める |
| Cosine(x座標) |
=COS(B2) |
|
| Sine(y座標) |
=SIN(B2) |
|
| Tangent(z座標) |
=TAN(B2) |
( = y / x ) |
| ARCCosine(角度) |
=DEGREES(ACOS(B3)) |
|
| ARCSine(角度) |
=DEGREES(ASIN(B4)) |
|
| ARCTangent(角度) |
=DEGREES(ATAN(B5)) |
( = y / x ) |
|
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
- セル「B1」の値(現在は「90」が入力されています)を変えてみて下さい。
|
|
|
- 三角関数が判れば逆三角関数の「アーク」はもっと簡単です。
- 前章のピタゴラスの定理:2章-2D編-図解の応用からです。
- 直角三角形3種類の1つ∠角と1つの辺で残りの辺を求める式です。
- 「三角関数を使う」という条件です。※算出方法は他にもあります。
- エクセルサンプルで説明します。
|
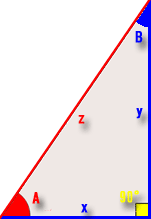 |
- 赤い部分が判っているところで青い部分が判らない箇所です。
- 黄色は∟(直角90度)です。
- ∠Aは「56.3」です。
- 辺zは「18.02775638」です。
- 「辺y」及び「辺x」を求める。
|
- 黄色の部分を選択するか
ボタンを押してエクセルのセル「A1」に「貼り付け」てみてください。
-
| |
A |
B |
C |
| 1 |
| 引数角度 |
56.3 |
∠A |
| RADIANS |
=RADIANS(B1) |
ラジアン |
| 引数正接 |
18.02775638 |
正接z |
| Sine |
=B3*SIN(B2) |
正弦y |
| Cosine |
=B3*COS(B2) |
余弦x |
|
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
|
|
|
|
|
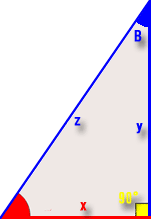 |
- 赤い部分が判っているところで青い部分が判らない箇所です。
- 黄色は∟(直角90度)です。
- ∠Aは「56.3」です。
- 辺xは「10.0026001668331」です。
- 「辺y」及び「辺z」を求める。
|
- 黄色の部分を選択するか
ボタンを押してエクセルのセル「A1」に「貼り付け」てみてください。
-
| |
A |
B |
C |
| 1 |
| 引数角度 |
56.3 |
∠A |
| RADIANS |
=RADIANS(B1) |
ラジアン |
| 引数余弦 |
10.0026001668331 |
余弦x |
| Cosine |
=B3/COS(B2) |
正接z |
| Tangent |
=B3*TAN(B2) |
正弦y |
|
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
|
|
|
|
|
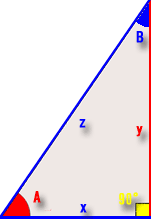 |
- 赤い部分が判っているところで青い部分が判らない箇所です。
- 黄色は∟(直角90度)です。
- ∠Aは「56.3」です。
- 辺zは「14.9982662331051」です。
- 「辺x」及び「辺z」を求める。
|
- 黄色の部分を選択するか
ボタンを押してエクセルのセル「A1」に「貼り付け」てみてください。
-
| |
A |
B |
C |
| 1 |
| 引数角度 |
56.3 |
∠A |
| RADIANS |
=RADIANS(B1) |
ラジアン |
| 引数正弦 |
14.9982662331051 |
正弦y |
| Sine |
=B3/SIN(B2) |
正接z |
| Tangent |
=B3/TAN(B2) |
余弦x |
|
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
|
|
|
|
|
|
|
- いよいよアークです。
- 「三角関数を使う」という条件です。※算出方法は他にもあります。
- エクセルでのサンプルです。
|
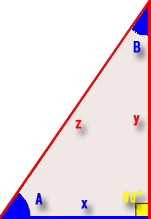 |
- 赤い部分が判っているところで青い部分が判らない箇所です。
- 黄色は∟(直角90度)です。
- 辺yは「14.9982662331051」です。
- 辺zは「18.02775638」です。
- 「∠A角度」及び「辺x」を求める。
- ヒントは前項のピタゴラスの定理:2章-2D編-図解での
- 縦位置(Y座標・正弦)÷斜位置(Z座標・正接)=Sine(サイン・正弦)。
- 縦位置(Y座標・正弦)と斜位置(Z座標・正接)が判っているのでARCSine(サイン・正弦)を使う。
|
- 黄色の部分を選択するか
ボタンを押してエクセルのセル「A1」に「貼り付け」てみてください。
-
| |
A |
B |
C |
| 1 |
| 引数正弦 |
14.9982662331051 |
正弦y |
| 引数正接 |
18.02775638 |
正接z |
| ARCSine |
=ASIN(B1/B2) |
ラジアン |
| DEGREES |
=DEGREES(B3) |
ディグリー |
| Cosine |
=B2*COS(RADIANS(B4)) |
余弦x |
| Tangent |
=B1/TAN(RADIANS(B4)) |
余弦x |
|
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
|
|
|
|
|
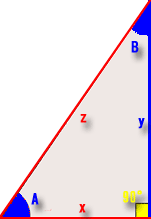 |
- 赤い部分が判っているところで青い部分が判らない箇所です。
- 黄色は∟(直角90度)です。
- 辺xは「10.0026001668331」です。
- 辺zは「18.02775638」です。
- 「∠A角度」及び「辺y」を求める。
- ヒントは前項のピタゴラスの定理:2章-2D編-図解での
- 横位置(X座標・余弦)÷斜位置(Z座標・正接)=Cosine(コサイン・余弦)。
- 横位置(X座標・余弦)と斜位置(Z座標・正接)が判っているのでARCCosine(コサイン・余弦)を使う
|
- 黄色の部分を選択するか
ボタンを押してエクセルのセル「A1」に「貼り付け」てみてください。
-
| |
A |
B |
C |
| 1 |
| 引数余弦 |
10.0026001668331 |
余弦x |
| 引数正接 |
18.02775638 |
正接z |
| ARCCosine |
=ACOS(B1/B2) |
ラジアン |
| DEGREES |
=DEGREES(B3) |
ディグリー |
| Tangent |
=B1*TAN(RADIANS(B4)) |
正弦y |
| Sine |
=B2*SIN(RADIANS(B4)) |
正弦y |
|
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
|
|
|
|
|
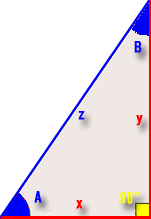 |
- 赤い部分が判っているところで青い部分が判らない箇所です。
- 黄色は∟(直角90度)です。
- 辺xは「10.0026001668331」です。
- 辺yは「14.9982662331051」です。
- 「∠A角度」及び「辺z」を求める。
- ヒントは前項のピタゴラスの定理:2章-2D編-図解での
- 縦位置(Y座標・正弦)÷横位置(X座標・余弦)=Tangent(タンジェント・正接)。
- 縦位置(Y座標・正弦)と横位置(X座標・余弦)が判っているのでARCTangent(タンジェント・正接)を使う
|
- 黄色の部分を選択するか
ボタンを押してエクセルのセル「A1」に「貼り付け」てみてください。
-
| |
A |
B |
C |
| 1 |
| 引数余弦 |
10.0026001668331 |
余弦x |
| 引数正弦 |
14.9982662331051 |
正弦y |
| ARCTangent |
=ATAN(B2/B1) |
ラジアン |
| DEGREES |
=DEGREES(B3) |
ディグリー |
| Sine |
=B2/SIN(RADIANS(B4)) |
正接z |
| Cosine |
=B1/COS(RADIANS(B4)) |
正接z |
|
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
|
|
|
|
|
|











